发表于 | 分类于 | 阅读次数:
字数统计: 262

一：选择排序的基本介绍

​ 选择式排序也属于内部排序法，是从欲排序的数据中，按指定的规则选出某一元素，在依规定交换位置后达到排序的目的。

二：选择排序思想

1574408865064

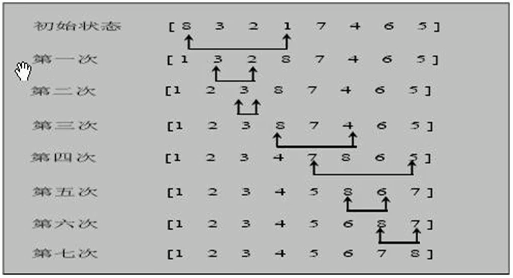
1574409160331

1574409316773

三：选择排序应用实例

有一群牛，颜值分别是101，34，119，100，1，请使用选择排序从低到高进行排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
static void Main(string[] args)
      {
          int[] arr = {101,34,119,1 };
          selectSort(arr);

      }
      //选择排序
      public static void selectSort(int[] arr)
      {
          for (int j = 0; j < arr.Length; j++)
          {
              int min = arr[j];
              int index = j;
              for (int i = j+1; i < arr.Length; i++)
              {
                  if (arr[i] < min)
                  {
                      index = i;
                      min = arr[i];
                  }
              }
              if (index != j)
              {
                  arr[index] = arr[j];
                  arr[j] = min;
              }
              
              Console.WriteLine("第{0}轮排序：",j+1);
              print(arr);
          }
         

      }
      public static void print(int[] arr)
      {
          for (int i = 0; i < arr.Length; i++)
          {
              Console.Write(arr[i]+"\t");
          }
          Console.WriteLine("");
      }

四：比较排序的效率

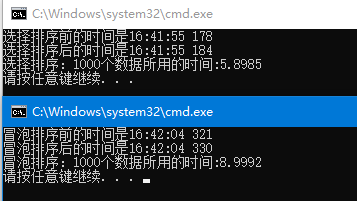
1574412140012

选择排序要比冒泡排序快

五：源码地址

Github源码地址

发表于 | 分类于 | 阅读次数:
字数统计: 617

一：冒泡的基本介绍

1574404458830

1574404494676

二：实际应用

1574404976105

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
static void Main(string[] args)
        {
            int[] arr = {3,9,-1,10,20 };
            for (int i = 0; i < arr.Length - 1; i++)
            {
                for (int j = 0; j < arr.Length - 1 - i; j++)
                {
                    if (arr[i] < arr[j])
                    {
                        int temp = arr[i];
                        arr[i] = arr[j];
                        arr[j] = temp;
                    }
                }
                Console.Write("第" + (i + 1) + "趟排序后的数组：");
                print(arr);
            }
            Console.WriteLine("最后的结果:");
            print(arr);

        }

        public static void print(int[] arr)
        {
            for (int i = 0; i < arr.Length; i++)
            {
                Console.Write(arr[i] + "\t");
            }
            Console.WriteLine("");
        }

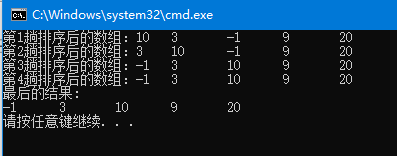
1574405291917

三：优化冒泡排序

引入一个开关，如果此次遍历没有交换值，说明顺序是正确，后面没必要重新多次遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
     static void Main(string[] args)
    {
        int[] arr = {3,9,-1,10,20 };
        bool flag = false;//标识变量，表示是否进行交换
   for (int i = 0; i < arr.Length - 1; i++)
    {
        for (int j = 0; j < arr.Length - 1 - i; j++)
        {
                if (arr[j] > arr[j+1])
                {
                    flag = true;
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
        }
        Console.Write("第" + (i + 1) + "趟排序后的数组：");
        print(arr);

        if (flag)//在一趟排序中，依次交换都没有发生过
        {
            flag = false;//重置flag，进行下次判断
        }
        else
        {
            break;
        }
    }
    Console.WriteLine("最后的结果:");
    print(arr);

}

public static void print(int[] arr)
{
    for (int i = 0; i < arr.Length; i++)
    {
        Console.Write(arr[i] + "\t");
    }
    Console.WriteLine("");
}

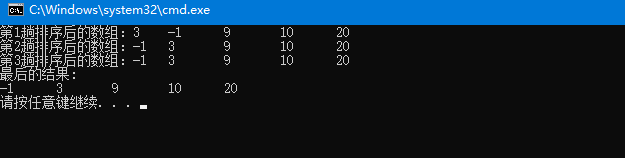
1574406293361

想比较上面的写法，减少了一次遍历。

四：比较排序的效率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
         int len = 10;//修改数据量
         int[] arrs = new int[len];
         for (int i = 0; i < len; i++)
         {
             Random random = new Random();
             int a = (int)random.Next(0, len);
             arrs[i] = a;
             Thread.Sleep(1);
         }
         Console.WriteLine("排序前的时间是"+DateTime.Now.ToString("HH:mm:ss fff"));
         bubbleSort(arrs);
         Console.WriteLine("排序后的时间是" + DateTime.Now.ToString("HH:mm:ss fff"));
         
         
public static void bubbleSort(int[] arr)
       {
         bool flag = false;//标识变量，表示是否进行交换
         for (int i = 0; i < arr.Length - 1; i++)
         {
             for (int j = 0; j < arr.Length - 1 - i; j++)
             {
                 if (arr[j] > arr[j + 1])
                 {
                     flag = true;
                     int temp = arr[j];
                     arr[j] = arr[j + 1];
                     arr[j + 1] = temp;
                 }
             }
           //  Console.Write("第" + (i + 1) + "趟排序后的数组：");
           //  print(arr);

             if (flag)//在一趟排序中，依次交换都没有发生过
             {
                 flag = false;//重置flag，进行下次判断
             }
             else
             {
                 break;
             }
         }
     }

10个数据冒泡排序比骄1000个数据：

1574408097405

1574408162091

当数据量越大，所需要的时间越长！

五：源码地址

Github冒泡源码

发表于 | 分类于 | 阅读次数:
字数统计: 462

一：排序算法介绍

排序：排序是将一组数据，依指定的顺序进行排列的过程

排序分类：

  1. 内部排序：指将需要处理的所有数据都加载到内部存储器中进行排序。

  2. 外部排序：数据量过大，无法全部加载到内存中，需要借助外部存储进行排序。

  3. 常见的排序算法分类：

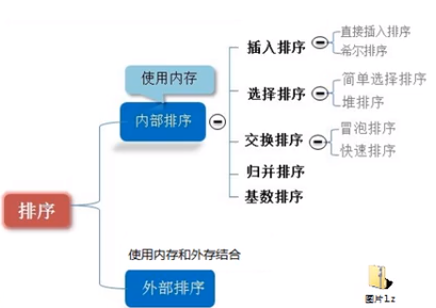
    1574397711743

二：算法的时间复杂度

1. 度量一个程序执行时间的两种方法

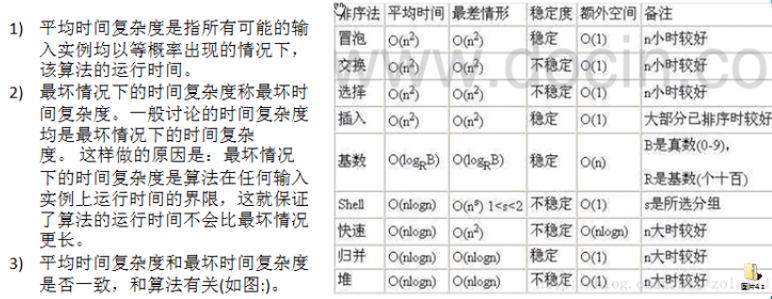
  1. 时候统计的方法

    这种方法可行，但是有两个问题：一是想对设计的算法的运行性能进行评测，需要实际运行该程序；二是所得时间的统计量依赖于计算机的硬件下、软件等环境因素，这种方式，要在同一台计算机的相同状态下运行，才能 比较哪个算法速度更快。

  2. 事前估算的方法

    通过分析某一个算法的时间复杂度来判断哪个算法更优。

2. 算法的时间复杂度：

1.时间频度：

一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)

​ 举例说明：

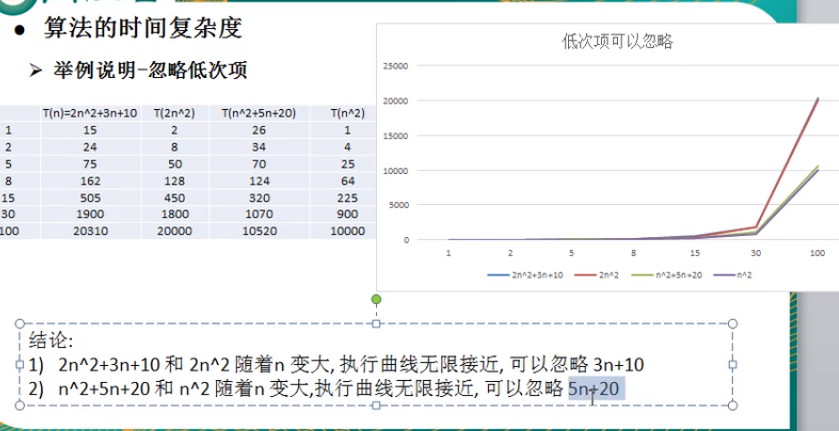
特点：

  • 常数项可以忽略
  • 低次项可以忽略
  • 系数可以忽略

2.时间复杂度：

1574398935149

3.常见的时间复杂度：

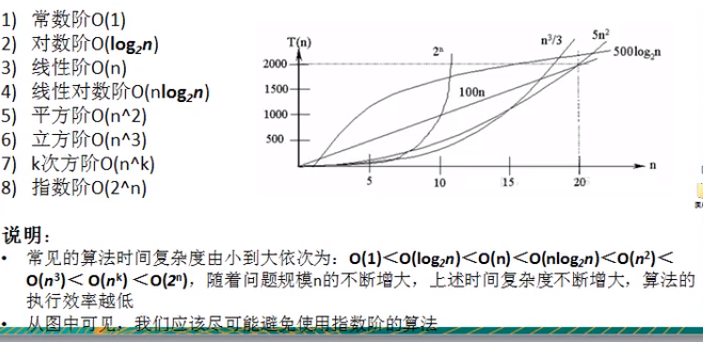
1574399244807

1. 常数阶O1

1574399448243常数阶O1

2.对数阶O(log2n)

1574399523713

3.线性阶O(n)

1574399793342

4.线性对数阶O(nlogN)

1574399854214

5.平方阶O(n*n)

1574399930968

6.立方阶O(nxnxn),K次方阶O(nxxxx…xxxxk)

1574400084147

4.平均时间复杂度和最坏时间复杂度

1574400386538

三：算法的空间复杂度

1574404100174

发表于 | 分类于 | 阅读次数:
字数统计: 376

一：问题介绍

1574389244278

二： 思路分析

1574389351792

三：代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
//定义一个max表示有多少皇后
     public static int max = 8;
      //定义数组array,保存皇后的位置的结果
      public static int[] array = new int[max];
      public static int count = 0;

      //编写一个方法，放置第n个皇后
      public void check(int n)
      {
          //判断是否放完了8个皇后
          if (n==max)
          {
              print();
          }
          else
          {
              //依次放入皇后，并判断是否冲突
              for (int i = 0; i < max; i++)
              {
                  //先吧当前 这个皇后n,放到该行的第1列
                  array[n] = i;
                  if (judge(n))//不冲突
                  {
                      check(n+1);
                  }
                  else
                  {
                      //如果冲突，就继续执行array[n]=i;
                  }
              }
          }
      }


      //查看当我们放置第n个皇后，就去检查该皇后是否和前面已经摆放的皇后冲突
      public bool judge(int n)
      {
          for (int i = 0; i < n; i++)
          {
              //判断是否在同一列、同一斜线
              //1.array[i]==array[n]判断是否在同一列
              //2.Math.Abs(n-i)==Math.Abs(array[n]-array[i])判断第n个皇后是否和第i个皇后在同一斜线
              if (array[i]==array[n]||Math.Abs(n-i)==Math.Abs(array[n]-array[i]))
              {
                  return false;
              }
          }
          return true;
      }
      //写个方法，将皇后的位置输出
      public void print()
      {
          for (int i = 0; i < array.Length; i++)
          {
              Console.Write(array[i]);
          }
          Console.WriteLine("");
          count++;
      }
  }
    static void Main(string[] args)
      {
          Queue8 queue = new Queue8();
          queue.check(0);
          Console.WriteLine("一共有{0}解法", Queue8.count);
      }

1574391370587

四：源码地址

Github八皇后问题解法–回溯

发表于 | 分类于 | 阅读次数:
字数统计: 661

一：介绍递归

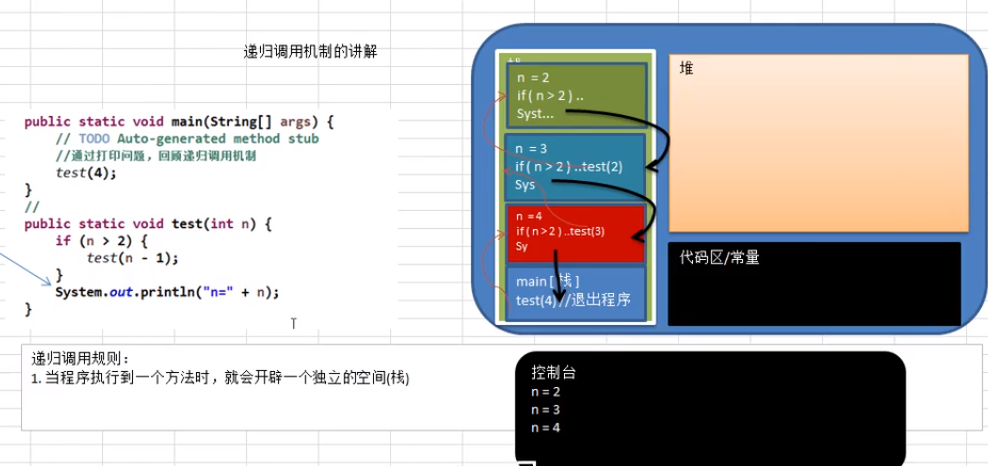
递归就是方法自己调用自己，每次调用时传入不同的变量，递归有助于编程者解决复杂问题。

二：递归调用机制

  1. 打印问题

    1
    2
    3
    4
    5
    6
    7
    8
    public static void test(int n)
          {
              if (n>2)
              {
                  test(n-1);
              }
              Console.WriteLine(n);
          }

1574339694068

三：递归需要遵循的重要规则

1574340640653

四：实际应用

递归-迷宫问题

1574343800156

五：代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
//使用递归回溯来给小球栈路
       //说明
       //1.map表达式地图
       //2.i,j表示地图的哪个位置开始出发（1，1）
       //3.如果小球能到map[6][5]位置，则说明通路找到
       //4.约定：当map[i][j]为0表示该点没有走过当为1.表示墙；2.表示通路可以走；3.表示该带你已经走过，但是走不通
       //5.在走迷宫时，需要确定一个策略下-》右-》上-》左

       /// <summary>
       /// 使用递归回溯给小球找路
       /// </summary>
       /// <param name="map">地图</param>
       /// <param name="i">从i位置开始找</param>
       /// <param name="j">从j位置开始找</param>
       /// <returns>如果找到通路，就返回true,否则返回false</returns>
       public static bool setway(int[,] map,int i,int j)
       {
           if (map[6,5]==2)
           {
               return true;
           }
           else
           {
               if (map[i,j]==0)//如果当前这个点还没有走过
               {
                   //策略下-》右-》上-》左
                   map[i, j] = 2;//假定该点是可以走通。
                   //向下
                   if (setway(map,i+1,j))
                   {
                       return true;
                   }
                   //向右
                   else if (setway(map, i, j+1))
                   {
                       return true;
                   }
                   //向上
                   else if (setway(map, i - 1, j))
                   {
                       return true;
                   }
                   //向左
                   else if (setway(map, i, j-1))
                   {
                       return true;
                   }
                   else
                   {
                       //该点走不通
                       map[i, j] = 3;
                       return false;
                   }
               }
               else
               {
                   //如果mao[i][j]!=0,可能1：墙，2：已走过，3：死路
                   return false;

               }
           }
       }
       
       
         static void Main(string[] args)
       {
           #region 迷宫
           //创建一个二维数组，模拟迷宫
           int[,] map = new int[8,7];
           //使用1表示墙
           //先把上下全部设置为1
           for (int i = 0; i < 7; i++)
           {
               map[0, i] = 1;
               map[7, i] = 1;
           }
           //左右设置为1
           for (int i = 0; i < 8; i++)
           {
               map[i, 0] = 1;
               map[i, 6] = 1;
           }
           //设置挡板，1
           map[3, 1] = 1;
           map[3, 2] = 1;

           Console.WriteLine("原地图：");
           //输出地图
           for (int i = 0; i < 8; i++)
           {
               for (int j = 0; j < 7; j++)
               {
                   Console.Write(map[i,j]+"\t");
               }
               Console.WriteLine("");
           }
           Console.WriteLine("----------------------------------------------------------");
           Console.WriteLine("找完迷宫的地图：");
           setway(map, 1, 1);
           for (int i = 0; i < 8; i++)
           {
               for (int j = 0; j < 7; j++)
               {
                   Console.Write(map[i, j] + "\t");
               }
               Console.WriteLine("");
           }
           #endregion
       }

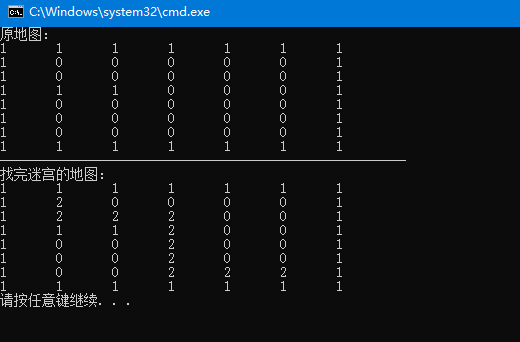
1574343878260

六：源码地址

GitHub源码地址

发表于 | 分类于 | 阅读次数:
字数统计: 691

一：思路分析

  1. 初始化两个栈：运算符栈s1和储存中间结果的栈s2

  2. 从左至有扫描中缀表达式

  3. 遇到操作数时，将其压入s2

  4. 遇到运算符时，比较其与s1栈顶运算符的优先级：

    1. 如果s1为空，或栈顶运算符为左括号“(”，则直接将次运算符入栈
    2. 否则，若优先级比较栈顶运算符的高，也将运算符压入s1
    3. 否则，将s1栈顶的运算符弹出并压入到s2中，再次将（4-1）与s1中心耳朵栈顶运算符想比较

  5. 遇到括号时：

    1. 如果是左括号“(”，则直接压入s1
    2. 如果是右括号“)”,则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃

  6. 重复2至5，直到表达式的最右边

  7. 将s1中剩余的运算符依次弹出并压入s2

  8. 依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

    1
    中缀表达式1+((2+3)*4)-5==>后缀表达式123+4*+5-

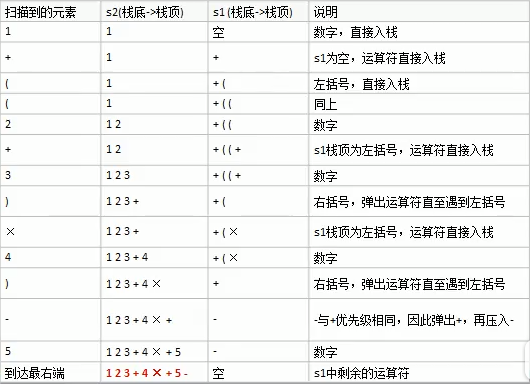
1574172008981

二：代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
public List<string> parseSuffixExpressionList(List<string> ls)
    {
        //定义两个栈
        Stack<string> s1 = new Stack<string>();//符号栈
   //  Stack<string> s2 = new Stack<string>();//数值栈[只有入栈，没有出栈]
        List<string> s2 = new List<string>();
        string str = "";
        foreach (var item in ls)
        {
            Regex regExp = new Regex("^\\d+$");//匹配的是多位数
          
            if (regExp.IsMatch(item))
            {
                //如果是数字
                //入栈
                s2.Add(item);
            }
            else if(item=="(")
            {
                s1.Push(item);
            }
            else if (item==")")
            {
                while (s1.Peek()!="(")
                {
                    s2.Add(s1.Pop());
                }
                s1.Pop();//!!!将（弹出s1栈
            }
            else
            {
                //当item小于等于栈顶运算符，将s1栈顶的运算符弹出并加入s2中，再次转到4.1与s1中心的栈顶运算符想比较
                while (s1.Count != 0 && Operation.getValue(s1.Peek())>= Operation.getValue(item))
                {
                    s2.Add(s1.Pop());
                }
                //还需要将item压入栈中
                s1.Push(item);
            }
        }
        //将s1中剩余的运算符依次弹出并加入s2
        while (s1.Count()!=0)
        {
            s2.Add(s1.Pop());
        }
        return s2;
    }
    class Operation
    {
        private static int ADD = 1;
        private static int SUB = 1;
        private static int MUL = 2;
        private static int DIV = 2;

        public static int getValue(string operation)
        {
            int result = 0;
            switch (operation)
            {
                case "+":
                    result = ADD;
                break;
                case "-":
                    result = SUB;
                    break;
                case "*":
                    result = MUL;
                    break;
                case "/":
                    result = DIV;
                    break;
                default:
                    Console.WriteLine("不存在该运算符！");
                    break;
            }
            return result;
        }
    }

}

//测试方法
void Main()
{
        string str = "1+((3+2)*4)-5";
        List<string> list = poland.toInfixExpressionList(str);
        
        List<string> list2 = poland.parseSuffixExpressionList(list);
        Console.Write("后缀表达式：");
        for (int i = 0; i < list2.Count; i++)
        {
            Console.Write(list2[i]);
        }
        Console.WriteLine("结果："+poland.calculate(list2));
}

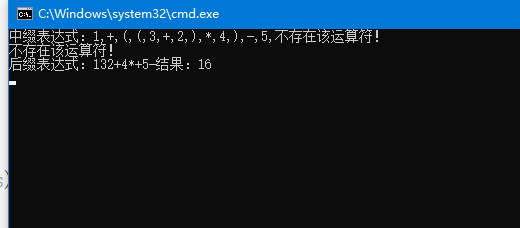
1574338060371

三：地址源码

GitHub源码

发表于 | 分类于 | 阅读次数:
字数统计: 196

一：思路分析

1574155612427

二：代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public class PolandNotation
    {
        public List<string> getListString(string suff)
        {
            string[] split = suff.Split(' ');
            List<string> list = new List<string>();
            foreach (var item in split)
            {
                list.Add(item);
            }
            return list;
        }
        public int calculate(List<string> list)
        {
            Stack<string> stack = new Stack<string>();
            foreach (var item in list)
            {
                Regex regExp = new Regex("^\\d+$");//匹配的是多位数
               
                if (regExp.IsMatch(item))
                {
                    //入栈
                    stack.Push(item);
                }
                else
                {
                    int num2 = Convert.ToInt32(stack.Pop());
                    int num1 = Convert.ToInt32(stack.Pop());
                    int res = 0;
                    if (item=="+")
                    {
                        res = num1 + num2;
                    }
                    else if (item == "-")
                    {
                         res = num1 - num2;
                    }
                    else if (item == "*")
                    {
                        res = num1 * num2;
                    }
                    else if (item == "/")
                    {
                        res = num1 / num2;
                    }
                    else
                    {
                        throw new Exception("运算符有问题！ ");
                    }
                    //把res入栈
                    stack.Push(""+res);
                }
            }

            return Convert.ToInt32(stack.Pop());
        }
    }

三：源码地址

Github

发表于 | 分类于 | 阅读次数:
字数统计: 237

一：前缀、中缀、后缀表达式【逆波兰表达式】

1.前缀表达式又称为波兰式，前缀表达式的运算符位于操作数之前

举例说明：

1
（3+4）*5-6

对应的前缀表达式就是 

1
-*+3456

前缀 表达式的计算机求值

2.中缀表达式

1) .中缀表达式就是常见的运算表达式，如（3+4）*5-6

2).中缀表达式的求职是我们人最熟悉的，但是对计算机来说缺不好操作，因此，在计算结果时，往往会将中缀表达式转成其他表达式操作

3.后缀表达式

1.后缀表达式有称逆波兰表达式与前缀表达式像似，只是运算符位于操作数之后

2.举例说明：

1
（3+4）*5-6

对应的后缀表达式就是

1
34+5*6-

3.在对比：

1574145286618

后缀 表达式的计算机求值

1574145547711

发表于 | 分类于 | 阅读次数:
字数统计: 682

一：问题描述

使用栈计算：
$$
722-5+1-5+3-4的值，
$$
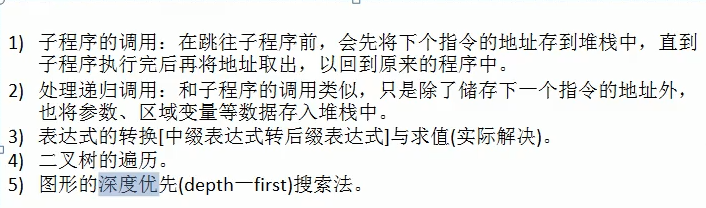
模拟计算机的底层操作！

二：思路分析

1574057233983

三：代码实现

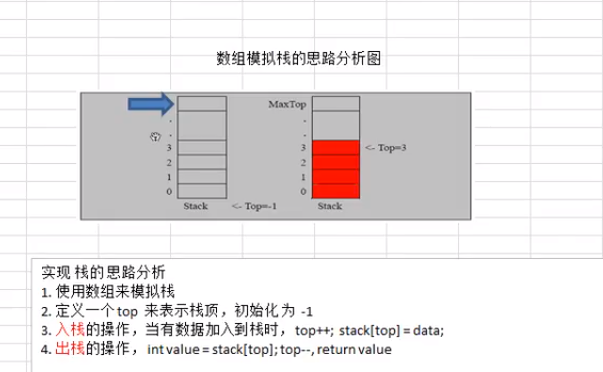
使用数组设置的栈：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
public class ArrayStack2
    {
        private int maxsize;//声明栈的长度
        private int top = -1;//栈顶
        private int[] stack;
        //构造器
        public ArrayStack2(int maxsize)
        {
            this.maxsize = maxsize;
            stack = new int[maxsize];
        }
        //栈满
        public bool isFull()
        {
            return top == maxsize - 1;
        }
        //栈空
        public bool isEmpty()
        {
            return top == -1;
        }
        //入栈-push
        public void push(int n)
        {
            if (isFull())
            {
                Console.WriteLine("栈满，无法添加！");
                return;
            }
            top++;
            stack[top] = n;
        }
        //出栈-pop
        public int pop()
        {
            if (isEmpty())
            {
                throw new Exception("栈空，无法出栈！");
            }
            int value = stack[top];
            top--;
            return value;
        }
        //遍历栈
        public void showlist()
        {
            if (isEmpty())
            {
                throw new Exception("栈空，无法出栈！");
            }
            for (int i = top; i >= 0; i--)
            {
                Console.WriteLine(pop());
            }
        }
        //返回运算符的优先级，优先级是程序员来确定。
        //优先级使用数字表示，数字越大优先级越高。
        public int priority(int oper)
        {
            if (oper=='*'||oper=='/')
            {
                return 1;
            }
            else if (oper == '+' || oper == '-')
            {
                return 0;
            }
            else
            {
                return -1;
            }
        }
        //判断是不是一个运算符
        public bool isOper(char val)
        {
            return val == '+' || val == '-' || val == '*' || val == '/';
        }
        //计算方法
        public int cal(int num1,int num2,int oper)
        {
            int res = 0;
            switch (oper)
            {
                case '+':
                    res= num1 + num2;
                    break;
                case '-':
                    res = num2 - num1;
                    break;
                case '*':
                    res = num1 * num2;
                    break;
                case '/':
                    res = num1 / num2;
                    break;
                default:
                    break;
            }
            return res;
        }
        //可以返回当前栈顶的值
        public int peek()
        {
            return stack[top];
        }
        
    }

在Main函数中执行：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
static void Main(string[] args)
      {
       #region 计算表达式(只能计算1-9的加、减、乘、除操作！)
          string str = "7+2*6-4*2";
          char[] vs = str.ToCharArray();
          //声明两个栈，一个存放数字，一个存放符合
          ArrayStack2 numstack = new ArrayStack2(10);
          ArrayStack2 operstack = new ArrayStack2(10);
          int index = 0;
          int num1 = 0;
          int num2 = 0;
          int oper = 0;
          int res = 0;
          char ch = ' ';
          while (true)
          {
              //依次得str的每一个字符
              ch = vs[index];
              //判断ch是什么，然后做相应的处理
              if (operstack.isOper(ch))
              {
                  //判断当前的字符栈是否为空
                  if (!operstack.isEmpty())
                  {
                      if (operstack.priority(ch) <= operstack.priority(operstack.peek()))
                      {
                          num1 = numstack.pop();
                          num2 = numstack.pop();
                          oper = operstack.pop();
                          res = numstack.cal(num1, num2, oper);
                          //入栈
                          numstack.push(res);
                          //当前符号入符号栈
                          operstack.push(ch);
                      }
                      else
                      {
                          operstack.push(ch);
                      }
                  }
                  else
                  {
                      //数字入栈
                      operstack.push(ch);
                  }
              }
              else
              {
                  numstack.push(ch - 48);
              }
              index++;
              if (index >= vs.Length)
              {
                  break;
              }
          }

          while (true)
          {
              //如果符号栈为空，则计算到最后的结果，数栈就是最终的结果
              if (operstack.isEmpty())
              {
                  break;
              }
              num1 = numstack.pop();
              num2 = numstack.pop();
              oper = operstack.pop();
              res = numstack.cal(num1, num2, oper);
              //入栈
              numstack.push(res);
          }

          Console.WriteLine("表达式：{0}的结果={1}", str, numstack.pop());
          #endregion

          Console.ReadKey();
      }

四：源码地址

Github源码地址

发表于 | 分类于 | 阅读次数:
字数统计: 487

一：介绍栈

  1. 栈的英文（stack）
  2. 栈是一个先入先出（FILO-First In Last Out）的有序列表。
  3. 栈（stack）是限制线性表中元素的插入和删除只能在线性表的同一个端机械能一种特殊线性表。允许插入和删除的一端，为变化的一端，称为栈顶（TOP),另一端为固定的一端，称为栈底（Bottom）。
  4. 根据栈的定义可知，最先放入栈中元素在栈底，最后放入的元素在栈顶，而删除元素刚好相反，最后放入的元素最先删除，最先放入的元素最后删除。

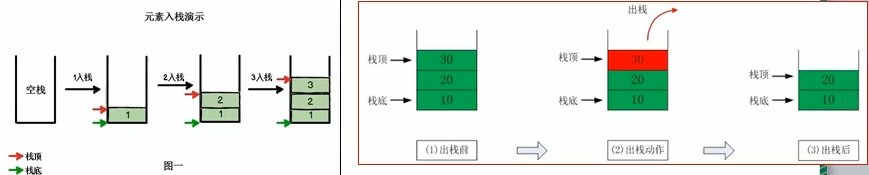
1574047858600

二：栈的引用场景

1574047995815

三:使用数组模拟栈

1574054079167

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class ArrayStack
  {
      private int maxsize;//声明栈的长度
      private int top = -1;//栈顶
      private int[] stack;
      //构造器
      public ArrayStack(int maxsize)
      {
          this.maxsize = maxsize;
          stack = new int[maxsize];
      }
      //栈满
      public bool isFull()
      {
          return top == maxsize - 1;
      }
      //栈空
      public bool isEmpty()
      {
          return top == -1;
      }
      //入栈-push
      public void push(int n)
      {
          if (isFull())
          {
              Console.WriteLine("栈满，无法添加！");
              return;
          }
          top++;
          stack[top] = n;
      }
      //出栈-pop
      public int pop()
      {
          if (isEmpty())
          {
              throw new Exception("栈空，无法出栈！");
          }
          int value=stack[top];
          top--;
          return value;
      }
      //遍历栈
      public void showlist()
      {
          if (isEmpty())
          {
              throw new Exception("栈空，无法出栈！");
          }
          for (int i = top; i >= 0; i--)
          {
              Console.WriteLine(pop());
          }
      }

四：使用链表模拟栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
public class LinkedStack
   {
       public Node head = new Node(-1);//虚拟头结点
       //链空
       public bool isEmpty()
       {
           return head.next == null;
       }
       //入栈
       public void push(int n)
       {
           Node temp = new Node(n);
           Node temp2 = head;
               while (temp2.next != null)
               {
                   temp2 = temp2.next;
               }
               temp2.next = temp;
        
       }
       //出栈
       public int pop()
       {
           Node temp =head;
           int value = 0;
           if (temp.next == null)
           {
               temp.next = null;
           }
           else
           {
               value = temp.next.no;
               temp.next = temp.next.next;
           }
           return value;
       }
       //展示列表
       public void showlist()
       {
           Node temp = head;
           if (isEmpty())
           {
               Console.WriteLine("栈空！");
           }
           while (temp.next!=null)
           {
               Console.WriteLine(pop());
               temp = temp.next;
           }
           Console.WriteLine(temp.no);
       } 
   }
   public class Node
   {
       public int no;
       public Node next;
       public Node(int no)
       {
           this.no = no;
       }
   }